Or you want a quick look: Nguyên hàm và tính chất
Traloitructuyen.com cũng giúp giải đáp những vấn đề sau đây:
- Chúng minh công thức nguyên hàm nâng cao
- Công thức nguyên hàm
- Công thức đạo hàm
- Công thức nguyên hàm từng phần
- Các phương pháp tính nguyên hàm
- Nguyên hàm từng phần
- nguyên hàm 1/u
- Tính chất nguyên hàm

Công thức nguyên hàm - Một số phương pháp tìm nguyên hàm
Công thức nguyên hàm không thể thiếu trong bộ môn giải tích lớp 12, cũng là một trong những khái niệm xuất hiện khá nhiều trong đề thi đại học.
Ở bài viết trước traloitructuyen.com đã chia sẻ công thức lượng giác. Ở bài viết này chúng tôi sẽ tiếp tục chia sẻ bảng công thức nguyên hàm cơ bản, từng phần, mở rộng, nâng cao.
- công thức nguyên hàm 1/x^2
- Chúng minh công thức nguyên hàm nâng cao
- công thức nguyên hàm ln(u)
- Công thức đạo hàm
- Công thức nguyên hàm từng phần
- Chứng minh công thức nguyên hàm
Nguyên hàm và tính chất
Nguyên hàm và tính chất
Khái niệm nguyên hàm
Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng của R.
Định nghĩa:
Cho hàm số f(x) xác định trên K.
Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F′(x)=f(x) với mọi x∈K.
Định lý 1:
Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x)=F(x)+C cũng là một nguyên hàm của hàm số f(x) trên K.
Định lý 2:
Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x)+C với C là một hằng số tùy ý.
Kí hiệu họ nguyên hàm của hàm số f(x) là ∫f(x)dx.
Khi đó :
Tính chất nguyên hàm
Tính chất 1: ∫f′(x)dx=f(x)+C,C∈R.
Tính chất 2: ∫fk(x)dx=k∫f(x)dx (với k là hằng số khác 0).
Tính chất 3: ∫(f(x)±g(x))dx=∫f(x)dx±∫g(x)dx.
Sự tồn tại của nguyên hàm
Định lí 3:
Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
Nguyên hàm của một số hàm số thường gặp
Nguyên hàm của các hàm số sơ cấp thương gặp:
∫kdx=kx+C,k∈R
∫xαdx=11+α.xα+1+C(α≠–1)
∫dxx=ln|x|+C
∫dxx=2x+C
∫exdx=ex+C
∫axdx=axlna+C(0<a≠1)
∫cosxdx=sinx+C
∫sinxdx=–cosx+C
∫dxcos2x=tanx+C
∫dxsin2x=–cotx+C
Ngoài ra còn có một số công thức thường gặp khác:
∫(ax+b)kdx=1a(ax+b)k+1k+1+C,(a≠0,k≠–1)
Một số phương pháp tìm nguyên hàm
.jpg)
Một số phương pháp tìm nguyên hàm
Phương pháp đổi biến
Đổi biến dạng 1
a. Định nghĩa.
Cho hàm số u = u(x) có đạo hàm liên tục trên K và hàm số y = f(u) liên tục sao cho f[u(x)] xác định trên K. Khi đó, nếu F là một nguyên hàm của f, tức là: ∫ f(u)du = F(u) + C thì:
∫ f[u(x)]u'(x)dx = F[u(x)] + C
b. Phương pháp giải
Bước 1: Chọn t = φ(x). Trong đó φ(x) là hàm số mà ta chọn thích hợp.
Bước 2: Tính vi phân hai vế: dt = φ'(t)dt.
Bước 3: Biểu thị: f(x)dx = f[φ(t)]φ'(t)dt = g(t)dt.
Bước 4: Khi đó: I = ∫ f(x)dx = ∫g(t)dt = G(t) + C.
Phương pháp đổi biến loại 2
a. Định nghĩa:
Cho hàm số f(x) liên tục trên K; x = φ(t) là một hàm số xác định, liên tục trên K và có đạo hàm là φ'(t). Khi đó, ta có:
∫ f(x)dx = ∫ f[φ(t)].φ'(t)dt
b. Phương pháp chung
Bước 1: Chọn x = φ( t), trong đó φ(t) là hàm số mà ta chọn thích hợp.
Bước 2: Lấy vi phân hai vế: dx = φ'(t)dt.
Bước 3: Biến đổi: f(x)dx = f[φ(t)]φ'(t)dt = g(t)dt.
Bước 4: Khi đó tính: ∫ f(x)dx = ∫g(t)dt = G(t) + C.
c. Các dấu hiệu đổi biến thường gặp

Phương pháp nguyên hàm từng phần
a. Định lí
Nếu u(x), v(x) là hai hàm số có đạo hàm liên tục trên K:
∫u(x).v'(x)dx = u(x).v(x) – ∫v(x).u'(x)dx
Hay ∫udv = uv – ∫vdu
(với du = u'(x)dx, dv = v'(x)dx)
b. Phương pháp chung
Bước 1: Ta biến đổi tích phân ban đầu về dạng: I = ∫ f(x)dx = ∫ f1(x).f2(x)dx
Bước 2: Đặt:

c. Các dạng thường gặp
Dạng 1
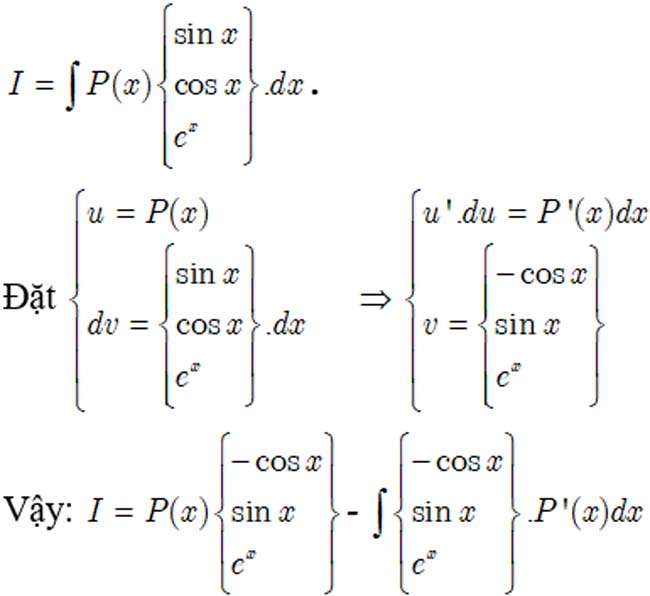
Dạng 2

Dạng 3

sau đó thay vào I.
Những điểm sai thường gặp khi giải toán liên quan đến bảng nguyên hàm

Những điểm sai thường gặp khi giải toán liên quan đến bảng nguyên hàm
Đa số khi giải dạng đề này các bạn thường mắc phải các sai lầm như:
– Hiểu sai bản chất công thức
– Cẩu thả, dẫn đến tính sai nguyên hàm
– Không nắm vững định nghĩa về nguyên hàm, tích phân
– Đổi biến số nhưng quên đổi cận
– Đổi biến không tính vi phân
– Không nắm vững phương pháp nguyên hàm từng phần
Dưới đây sẽ là một số lỗi sai cụ thể mà người giải đề thường xuyên gặp phải khi giải các đề toán liên quan đến bảng nguyên hàm. Các bạn hãy cùng theo dõi để tránh mắc phải tương tự nhé!
- Nhớ nhầm công thức của nguyên hàm
Nguyên nhân: nền tảng của nguyên hàm là đạo hàm. Tức là muốn giải được nguyên hàm trước tiên bạn cần học hoặc tìm hiểu về đạo hàm trước đã. Và cũng vì thế mà khi chưa hiểu rõ được bản chất của hai định nghĩa này bạn có thể dễ bị nhầm lẫn giữa cả hai, nhầm công thức này qua công thức kia.
Khắc phục: học vững bảng nguyên hàm cơ bản, luyện tập thói quen kiểm tra công thức: lấy đạo hàm của nguyên hàm tìm được xem có bằng số đề cho hay không.
- Không vận dụng đúng định nghĩa tích phân
Khắc phục: đọc và nắm kỹ định nghĩa tích phân. Tạo thói quen khi tính ∫f(x)dx nhớ chú ý kiểm tra xem hàm số y = f(x) có liên tục trên đoạn hay không. Lưu ý đặc biệt, nếu hàm số không liên tục trên đoạn thì nghĩa là tích phân đó không tồn tại!
- Nhớ nhầm tính chất tích phân nguyên hàm
Nguyên nhân: thay vì sử dụng công thức tích phân từng phần thì có nhiều bạn thường tự sáng tạo ra quy tắc nguyên hàm của một tích. Lỗi sai này rất nghiêm trọng nhưng cũng rất phổ biến.
Khắc phục: một lần nữa đọc lại và nắm vững tính chất của nguyên hàm và tích phân
- Vận dụng sai công thức nguyên hàm
Nguyên nhân: vì dạng đề và công thức bảng nguyên hàm rất nhiều nên nhiều trường hợp các bạn áp dụng sai công thức, hoặc nhớ nhầm từ công thức này sang công thức kia
Khắc phục: cẩn thận và tỉ mỉ là một yếu tố cực kỳ cần thiết dành cho môn toán, tại vì nhiều khi chỉ cần sai một con số nhỏ hoặc một công thức nhỏ trong bảng nguyên hàm nói riêng cũng như trong bài toán nói chung thì mọi kết quả sẽ trở nên công cốc.
Vì thế một lần nữa lời khuyên dành cho cách khắc phục các lỗi sai này là học thuộc vững bảng nguyên hàm và các công thức nguyên hàm cơ bản. Hiểu đúng dạng đề để tránh sử dụng sai công thức. Tính toán, áp số cẩn trọng, tránh những sai xót vặt vãnh.
Công thức nguyên hàm cơ bản thường gặp nhất


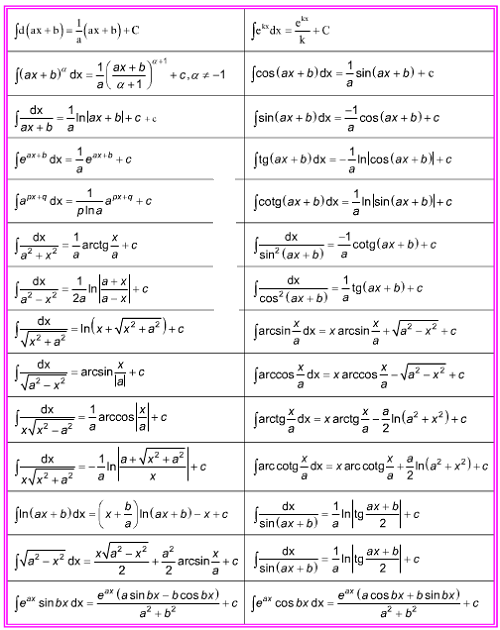
Bảng các nguyên hàm cơ bản

Bảng nguyên hàm mở rộng (a ≠ 0)


Thực ra, ta đã áp dụng tính chất sau đây: Nếu F(x) là một nguyên hàm của f(x) thì:

Bảng nguyên hàm nâng cao (a ≠ 0)

Định nghĩa, công thức Nguyên hàm
Định nghĩa
Cho hàm số f(x) xác định trên K (K là khoảng, đoạn hay nửa khoảng). Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F'(x) = f(x) với mọi x ∈ K.
Kí hiệu: ∫ f(x)dx = F(x) + C.
Định lí 1:
1) Nếu F(x) là một nguyên hàm của f(x) trên K thì với mỗi hằng số C, hàm số G(x) = F(x) + C cũng là một nguyên hàm của f(x) trên K.
2) Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x) + C, với C là một hằng số.
Do đó F(x) + C; C ∈ R là họ tất cả các nguyên hàm của f(x) trên K.
Tính chất của nguyên hàm
• (∫ f(x)dx)’ = f(x) và ∫ f'(x)dx = f(x) + C.
• Nếu F(x) có đạo hàm thì: ∫d(F(x)) = F(x) + C).
• ∫ kf(x)dx = k∫ f(x)dx với k là hằng số khác 0.
• ∫[f(x) ± g(x)]dx = ∫ f(x)dx ± ∫g(x)dx.
Sự tồn tại của nguyên hàm
Định lí:
Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.
Bảng nguyên hàm các hàm số thường gặp


Một số phương pháp tìm nguyên hàm
Phương pháp đổi biến
Đổi biến dạng 1
a. Định nghĩa.
Cho hàm số u = u(x) có đạo hàm liên tục trên K và hàm số y = f(u) liên tục sao cho f[u(x)] xác định trên K. Khi đó, nếu F là một nguyên hàm của f, tức là: ∫ f(u)du = F(u) + C thì:
∫ f[u(x)]u'(x)dx = F[u(x)] + C
b. Phương pháp giải
Bước 1: Chọn t = φ(x). Trong đó φ(x) là hàm số mà ta chọn thích hợp.
Bước 2: Tính vi phân hai vế: dt = φ'(t)dt.
Bước 3: Biểu thị: f(x)dx = f[φ(t)]φ'(t)dt = g(t)dt.
Bước 4: Khi đó: I = ∫ f(x)dx = ∫g(t)dt = G(t) + C.
Phương pháp đổi biến loại 2
a. Định nghĩa:
Cho hàm số f(x) liên tục trên K; x = φ(t) là một hàm số xác định, liên tục trên K và có đạo hàm là φ'(t). Khi đó, ta có:
∫ f(x)dx = ∫ f[φ(t)].φ'(t)dt
b. Phương pháp chung
Bước 1: Chọn x = φ( t), trong đó φ(t) là hàm số mà ta chọn thích hợp.
Bước 2: Lấy vi phân hai vế: dx = φ'(t)dt.
Bước 3: Biến đổi: f(x)dx = f[φ(t)]φ'(t)dt = g(t)dt.
Bước 4: Khi đó tính: ∫ f(x)dx = ∫g(t)dt = G(t) + C.
c. Các dấu hiệu đổi biến thường gặp

Phương pháp nguyên hàm từng phần
a. Định lí
Nếu u(x), v(x) là hai hàm số có đạo hàm liên tục trên K:
∫u(x).v'(x)dx = u(x).v(x) – ∫v(x).u'(x)dx
Hay ∫udv = uv – ∫vdu
(với du = u'(x)dx, dv = v'(x)dx)
b. Phương pháp chung
Bước 1: Ta biến đổi tích phân ban đầu về dạng: I = ∫ f(x)dx = ∫ f1(x).f2(x)dx
Bước 2: Đặt:

c. Các dạng thường gặp
Dạng 1
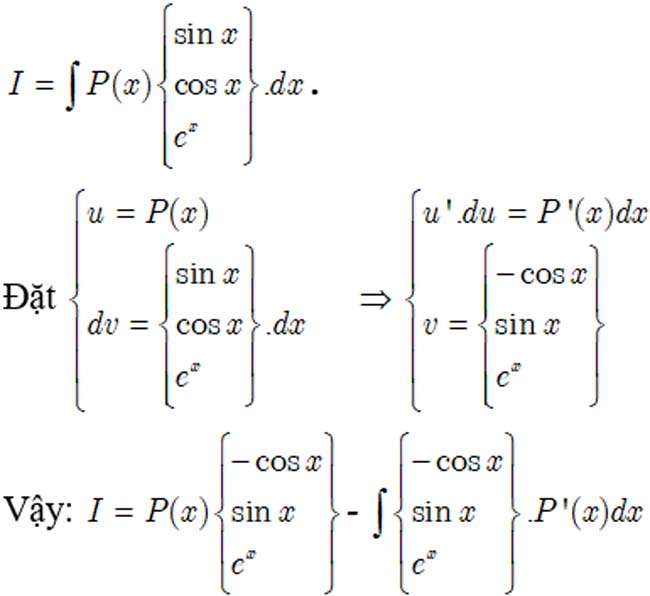
Dạng 2

Dạng 3

sau đó thay vào I.
Những điểm sai thường gặp khi giải toán liên quan đến bảng nguyên hàm
Đa số khi giải dạng đề này các bạn thường mắc phải các sai lầm như:
– Hiểu sai bản chất công thức
– Cẩu thả, dẫn đến tính sai nguyên hàm
– Không nắm vững định nghĩa về nguyên hàm, tích phân
– Đổi biến số nhưng quên đổi cận
– Đổi biến không tính vi phân
– Không nắm vững phương pháp nguyên hàm từng phần
Dưới đây sẽ là một số lỗi sai cụ thể mà người giải đề thường xuyên gặp phải khi giải các đề toán liên quan đến bảng nguyên hàm. Các bạn hãy cùng theo dõi để tránh mắc phải tương tự nhé!
- Nhớ nhầm công thức của nguyên hàm
Nguyên nhân: nền tảng của nguyên hàm là đạo hàm. Tức là muốn giải được nguyên hàm trước tiên bạn cần học hoặc tìm hiểu về đạo hàm trước đã. Và cũng vì thế mà khi chưa hiểu rõ được bản chất của hai định nghĩa này bạn có thể dễ bị nhầm lẫn giữa cả hai, nhầm công thức này qua công thức kia.
Khắc phục: học vững bảng nguyên hàm cơ bản, luyện tập thói quen kiểm tra công thức: lấy đạo hàm của nguyên hàm tìm được xem có bằng số đề cho hay không.
- Không vận dụng đúng định nghĩa tích phân
Khắc phục: đọc và nắm kỹ định nghĩa tích phân. Tạo thói quen khi tính ∫f(x)dx nhớ chú ý kiểm tra xem hàm số y = f(x) có liên tục trên đoạn hay không. Lưu ý đặc biệt, nếu hàm số không liên tục trên đoạn thì nghĩa là tích phân đó không tồn tại!
- Nhớ nhầm tính chất tích phân nguyên hàm
Nguyên nhân: thay vì sử dụng công thức tích phân từng phần thì có nhiều bạn thường tự sáng tạo ra quy tắc nguyên hàm của một tích. Lỗi sai này rất nghiêm trọng nhưng cũng rất phổ biến.
Khắc phục: một lần nữa đọc lại và nắm vững tính chất của nguyên hàm và tích phân
- Vận dụng sai công thức nguyên hàm
Nguyên nhân: vì dạng đề và công thức bảng nguyên hàm rất nhiều nên nhiều trường hợp các bạn áp dụng sai công thức, hoặc nhớ nhầm từ công thức này sang công thức kia
Khắc phục: cẩn thận và tỉ mỉ là một yếu tố cực kỳ cần thiết dành cho môn toán, tại vì nhiều khi chỉ cần sai một con số nhỏ hoặc một công thức nhỏ trong bảng nguyên hàm nói riêng cũng như trong bài toán nói chung thì mọi kết quả sẽ trở nên công cốc.
Vì thế một lần nữa lời khuyên dành cho cách khắc phục các lỗi sai này là học thuộc vững bảng nguyên hàm và các công thức nguyên hàm cơ bản. Hiểu đúng dạng đề để tránh sử dụng sai công thức. Tính toán, áp số cẩn trọng, tránh những sai xót vặt vãnh.
Hướng Dẫn Giải Bài Tập Toán Đại 12: Chương Nguyên Hàm Chọn Lọc
Giải bài tập Toán đại 12: Bài 1 trang 126
a. Hãy nêu định nghĩa nguyên hàm của hàm số cho trước f(x) trên một khoảng.
b. Phương pháp tính nguyên hàm từng phần là gì? Đưa ra ví dụ minh họa cho cách tính đã nêu.
Hướng dẫn giải:
a. Xét hàm số f(x) xác định trên tập xác định A.
Như vậy, hàm số F(x) gọi là nguyên hàm của hàm số f(x) trên A khi F(x) thỏa mãn: F’(x)= f(x) ∀ x ∈ A.
Cách tính nguyên hàm từng phần:
Cho hai hàm số u = u(x) và v = v(x) có đạo hàm liên tục trên A, khi đó:
∫u(x).v’(x)dx = u(x).v(x) – ∫v(x).u’(x)dx
Ta có thể viết gọn lại: ∫udv = uv – ∫vdv.
Ví dụ minh họa:

Kiến thức cần nhớ:
Nguyên hàm của một hàm số f(x) xác định trên tập A là một hàm số F(x) thỏa: F’(x)=f(x) với mọi x thuộc tập A. Có vô số hàm thỏa mãn đều kiện trên, tập hợp chúng sẽ thành họ nguyên hàm của f(x).
Khi sử dụng công thức nguyên hàm từng phần, nên lưu ý lựa chọn hàm u, v. Một số dạng thường gặp:

Giải bài tập Toán đại 12: Bài 2 trang 126
a. Nêu định nghĩa tích phân hàm số f(x) trên đoạn [a;b]
b. Tính chất của tích phân là gì? Ví dụ cụ thể.
Hướng dẫn giải:
a. Xét hàm số y = f(x) liên tục trên [a; b], gọi F(x) là nguyên hàm của f(x) trên [a;b]
Khi đó, tích phân cần tìm là hiệu F(b)-F(a), kí hiệu:

b. Tính chất của tích phân:

Kiến thức bổ sung:
+ Để tính một số tích phân hàm hợp, ta cần đổi biến, dưới đây là một số cách đổi biến thông dụng:

+ Nguyên tắc sử dụng đặt u, v khi dùng công thức tính phân từng phần, ưu tiên thứ tự sau khi chọn u: Logarit -> Đa thức -> Lượng giác = Mũ.

Giải bài tập Toán đại 12: Bài 3 trang 126
Tìm nguyên hàm của các hàm số đã cho dưới đây:
a. f(x)=(x-1)(1-2x)(1-3x)
b. f(x)= sin(4x).cos2(2x)

d. f(x) = (ex – 1)3
Hướng dẫn giải:
a. Ta có:
(x-1)(1-2x)(1-3x) = 6x3 – 11x2 + 6x – 1
Suy ra
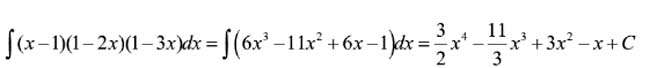
b. Ta có:

Suy ra:

c. Ta có:

Suy ra:

d. Đối với bài này, bạn đọc có thể theo cách giải thông thường là khai triển hằng đẳng thức bậc 3 rồi áp dụng tính nguyên hàm cho từng hàm nhỏ, tuy nhiên Kiến xin giới thiệu cách đặt ẩn phụ để giải tìm nguyên hàm.
Đặt t=ex
Suy ra: dt=exdx=tdx, vì vậy
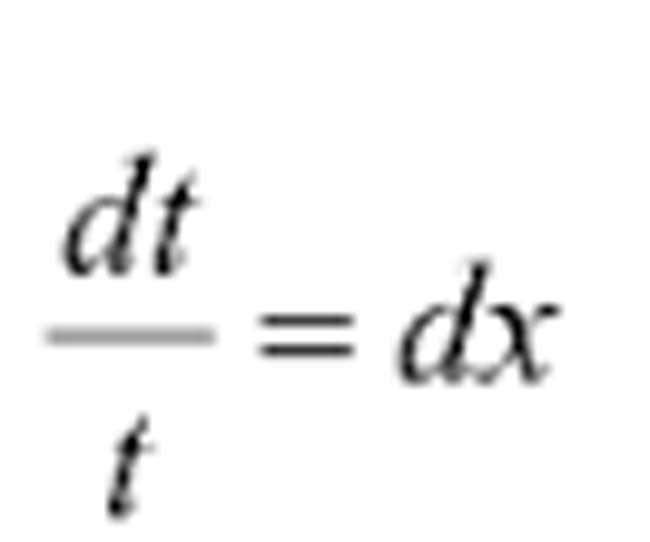
Ta sẽ có:


Với C’=C-1
Kiến thức cần nhớ:
Một số nguyên hàm thông dụng cần nhớ:

Giải bài tập Toán đại 12: Bài 4 trang 126
Tính một số nguyên hàm sau:

Hướng dẫn giải:



Kiến thức bổ sung
Một số công thức nguyên hàm thường gặp:
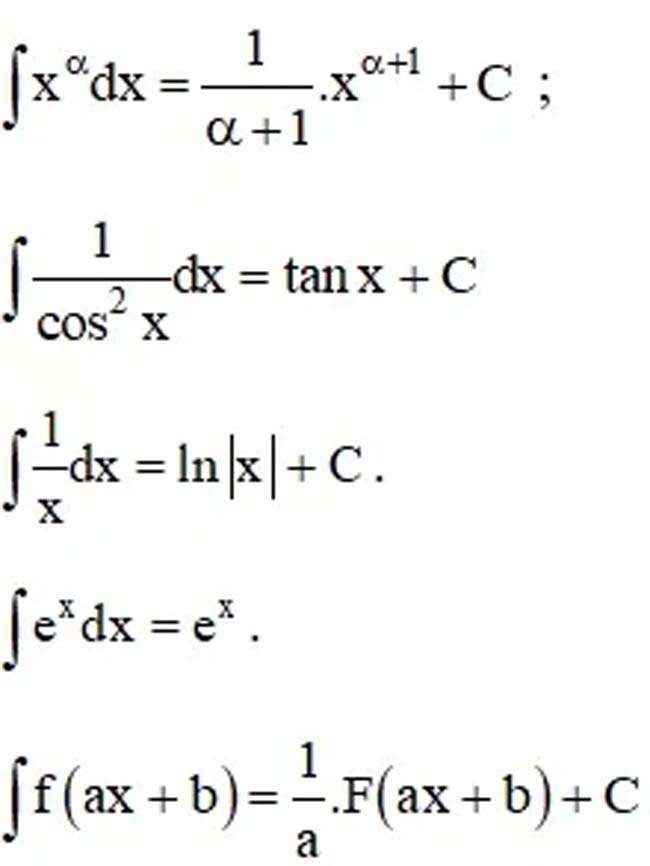
Giải bài tập toán đại 12 nâng cao
Đề THPT Chuyên KHTN lần 4:
Cho các số nguyên a, b thỏa mãn:

Tính tổng P=a+b?
Hướng dẫn giải:
Bài này là sự kết hợp tính tích phân của 1 hàm là tích của hai hàm khác dạng, kiểu (đa thức)x(hàm logarit). Vì vậy, cách giải quyết thông thường là sử dụng tích phân từng phần.
Ta có:

Đề thi thử Sở GD Bình Thuận:
Cho F(x) là một nguyên hàm của f(x). Biết rằng F(3)=3, tích phân: . Hãy tính:
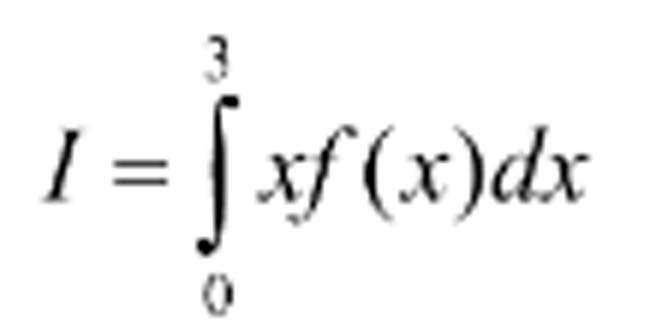
Hướng dẫn giải:
Đây là một dạng tính tích phân dạng hàm ẩn, tích phân cần tính lại là dạng 1 hàm số cụ thể nhân với 1 hàm chưa biết, như vậy cách giải quyết thường gặp sẽ là đặt ẩn phụ cho hàm, đồng thời sử dụng công thức tính tích phân từng phần.
Ở đây các bạn sẽ đặt: t=x+1, khi đó:

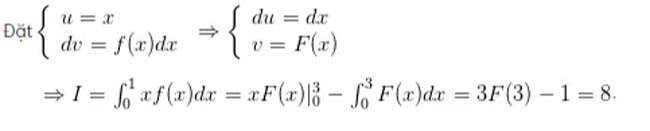
Kiến thức bổ sung:
+ Như vậy ở đây, một cách để nhận biết khi nào sẽ sử dụng tích phân từng phần là bài toán yêu cầu tính tích phân của hàm có dạng f(x).g(x), trong đó f(x) và g(x) là những hàm khác dạng nhau, có thể là hàm logarit, hàm đa thức, hàm mũ hoặc hàm lượng giác. Một số kiểu đặt đã được đề cập ở mục phía trước, bạn có thể tham khảo lại ở phía trên.
+ Một số công thức tính nguyên hàm của hàm vô tỷ:

Traloitructuyen.com cũng giúp giải đáp những vấn đề sau đây:
- Chúng minh công thức nguyên hàm nâng cao
- Công thức nguyên hàm
- Công thức đạo hàm
- Công thức nguyên hàm từng phần
- Các phương pháp tính nguyên hàm
- Nguyên hàm từng phần
- nguyên hàm 1/u
- Tính chất nguyên hàm
∫1ax+bdx=1aln|ax+b|+C,a≠0
∫eax+bdx=1aeax+b+C
∫cos(ax+b)dx=1asin(ax+b)+C
Các phương pháp tính nguyên hàm
Phương pháp đổi biến số
Định lí 1:
Cơ sở của phương pháp đổi biến số là định lý sau: Cho hàm số u=u(x) có đạo hàm và liên tục trên K và hàm số y=f(u) liên tục sao cho f[u(x)] xác định trên K. Khi đó nếu F là một nguyên hàm của f, tức là ∫f(u)du=F(u)+C thì ∫f[u(x)]dx=F[u(x)]+C.
Hệ quả:
Với u=ax+b(a≠0), ta có:
∫f(ax+b)dx=1aF(ax+b)+C
Phương pháp tính nguyên hàm từng phần
Định lí 2:
Nếu hai hàm số u=u(x) và v=v(x) có đạo hàm và liên tục trên K thì:
∫u(x)v′(x)dx=u(x)v(x)–∫u′(x)v(x)dx
Một số dạng thường gặp
Dạng 1: ∫P(x).eax+bdx,∫P(x)sin(ax+b)dx,∫P(x)cos(ax+b)dx
Cách giải: Đặt u=P(x),dv=eax+bdx hoặc dv=sin(ax+b)dx,dv=cos(ax+b)dx.
Dạng 2: ∫P(x)ln(ax+b)dx
Cách giải: Đặt u=ln(ax+b),dv=P(x)dx.
Bảng công thức nguyên hàm
Công thức nguyên hàm cơ bản

Công thức nguyên hàm cơ bản
Công thức nguyên hàm mở rộng

Công thức nguyên hàm mở rộng
Công thức nguyên hàm từng phần:

Công thức nguyên hàm từng phần
Công thức nguyên hàm nâng cao:

Công thức nguyên hàm nâng cao
Trên đây là bảng công thức nguyên hàm cơ bản, mở rộng, nâng cao mà chúng tôi tổng hợp giúp bạn nắm bắt kiến thức mới cũng như hệ thống lại kiến thức cũ tốt nhất. Nếu bạn còn câu hỏi hãy đặt ở bên dưới nhé.


